Markov Chain
Markov Chain refers to an approach that is based on probability theory using Markov models in order to model randomly changing systems when working with big data. From basic probability theory it is known that outcomes of previous events do not change the outcomes of future events. In practice however we know that this is not always correct and that there are events that are not independent in many applications.
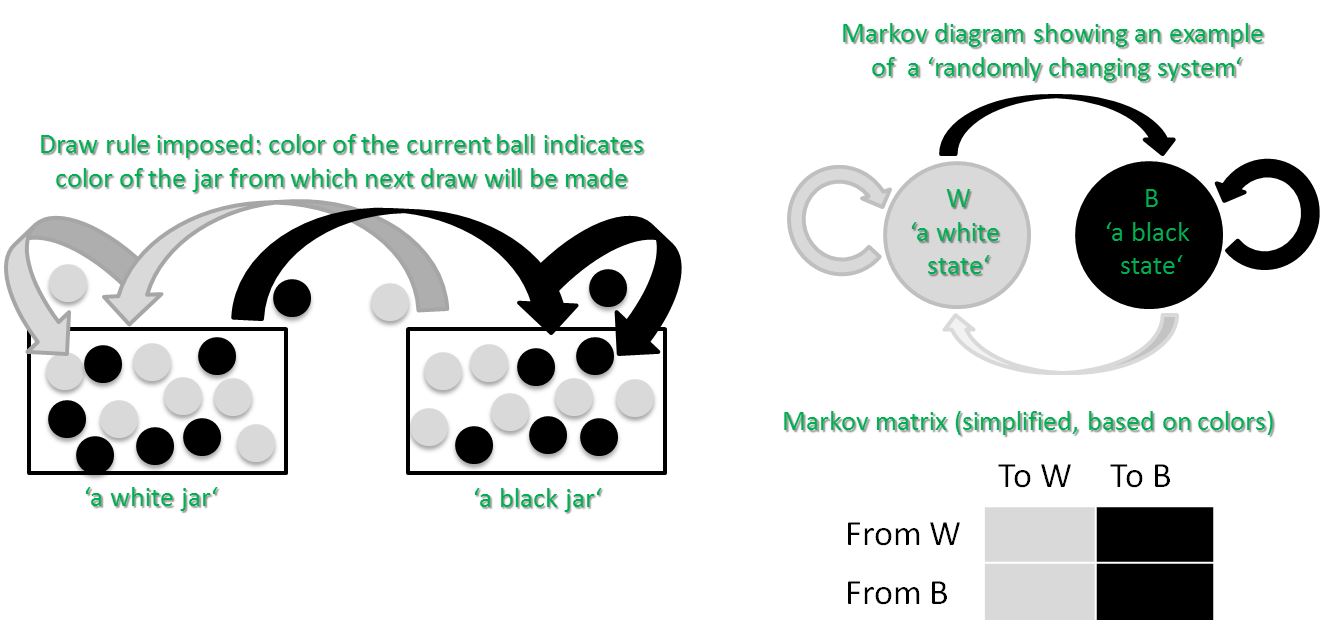
As a consequence the idea of a Markov chain is to add so-called dependent events and dependent variables. These dependent events and dependent variables refer to those situations when the probability of an event in the future is conditioned by the events that took place in the past. In other words one could think of it as adding an ‘events over time dimension‘. The figure above shows a two-state ‘Markov chain‘ that is the most basic Markov model that illustrates the Markov process. This figure also shows a simple example of the associated ‘Markov matrix‘ that is a stochastic matrix used to describe the transitions of a ‘Markov chain‘.









One key element of the Markov chain approach is known as the ‘Markov property’ of Markov models sometimes also called ‘memoryless property’. It refers to the idea that in order to make the prediction of what happens ‘tomorrow’ in time, we only need to consider what happens ‘today’ in time whereby the ‘past’ in time gives us no additional useful information. It slightly thus differentiates this model to machine learning models that try to learn as much as possible from historical data in order to make better decisions for the future.
Markov Chain Details
Please have a look on the following video for more details about the subject:











