Kernel
A choosen Kernel is one out of several so-called Kernel methods in machine learning that enable a smart use of non-linear decision boundaries. Such decision boundaries are often necessary since in many cases the given data is not linearly seperable. Non-linear transformations of the data are possible to make the data basically linear seperable, but instead the ‘kernel trick’ is often used in order to save time and efforts. This approach is often used in conjunction with Support Vector Machines and is described below while a basic understanding of non-linear transformations is essential in order to understand this approach better.
Understanding Non-linear Transformations
In order to use a linear decision boundary a non-linear transformation approach on the data itself can be performed. This is possible because in machine learning the data set in the input space are constants. One can use quadratic, cubic, or higher-order polynomial functions in order to transform the dataset. This means the feature space is enlarged but using these functions is computationally intensive. The figure below provides an example of performing a non-linear transformation with function Phi of data in the input space into a so-called feature space. The overall idea is to perform a given machine learning task (e.g. classification) in the new z-space or feature space. For instance, a classifier is trained on the transformed dataset. Then a classifier takes any new data point to classify, transforms it into the z-space, and uses a linear model with a linear decision boundary in the z-space for classification of the new point.
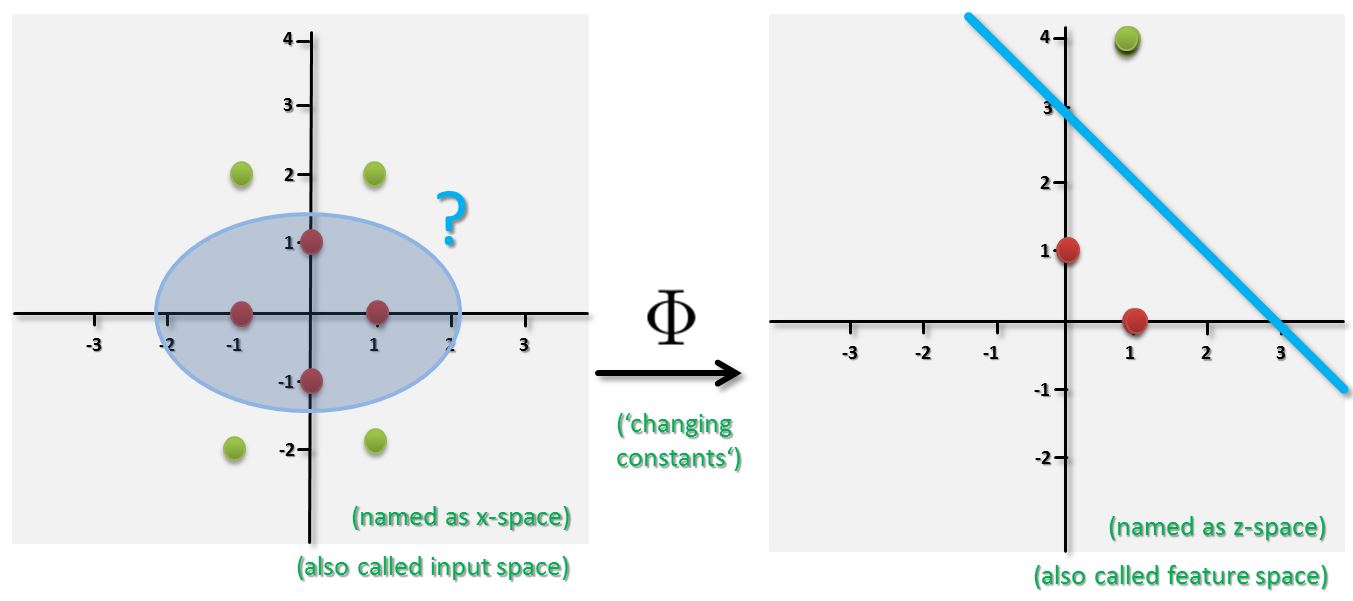
It is very important to understand that this process raises two elements of work. Firstly, (1) time investment is needed to find an appropriate mapping function Phi. Secondly, as this mapping is explicitly carried out on each data sample this process can be (2) computationally intensive. Especially when the non-linear Transformation leads to a high number of features the computations can even become unmanageable given big data sets. This further includes the danger to run into the so-called Problem ‘curse of dimensionality’ that is bad for learning from data.
Kernel
A kernel works exactly on these two particular elements of work and above mentioned problems in order to reduce the amount of work w.r.t. time and computing investments. The two dimensional example below shows that the dot product in the transformed space can be expressed in terms of a similarity function in the original space (here dot product is a similiarity between two vectors). Consider that you need first to (1) find an ideal mapping function Phi after a long search on your own. Afterwards the whole dataset needs to be mapped and transformed using (2) computational time using Phi as a mapping function for each sample. The example below however demonstrates the underlying idea of a kernel meaning that time can be saved by using the so-called kernel trick. By trusting a well known kernel function the dataset does not need to be transformed and explicitly be computed (red box in figure below) except the dot product that we obtain as a result that is much less computation.

More information about a kernel
The following video provides a good graphical illustration of how a kernel works:
Follow us on Facebook:











