Probability Measure

Probability measure is a measure of how likely a future ‘event’ is when analyzing big data with various models such as in statistical learning theory in general and as an example a Markov Chain in particular. The key question of this measure is thus ‘how likely a future event’ is and is a key element in probability theory that in turn has roots in gambling. There is a wide variety of research in understanding uncertainty in many application fields. Examples include the understanding of odds as the ratio of favorable or unfavorable outcomes. Further examples include the probability connected to dices, cards, coins, marbles, or balls.

One particular well known example is the probability of getting a white or a black ball out of one jar or multiple jars with different colors as shown below. After many random draws or trials from the jar, the observations as white balls vs. black balls will converge toward the real ratio of elements meaning the ratio white balls vs. black balls in the jars. Consider the situation below with an unknown number of X black balls and Y white balls within a jar. We want to have probability measure determining the proportions of black balls and white balls. The approach is to perform a series of random ‘draws’ or ‘trials’ from the jar. The ‘expected value’ of white vs. black draws will converge toward the real ratio from the jar as the number of extractions increases.

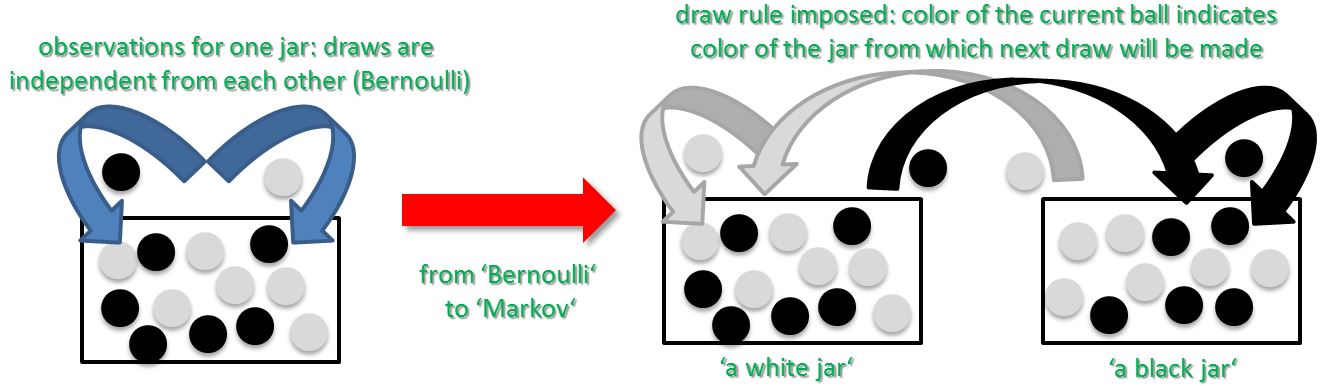
The figure above shows on the left side a typical scenario with one jar out of the probability theory. In this context do the outcomes of previous events not change the outcome of future events. It is important to understand that, in contrast to the left side, the right side has a draw rule imposed as a practice example. In the latter case are the events not independent as in many application areas. A more detailed description is available in our Markov Chain article.

Probability Measure Details

We recommend to look the following video for more details: