R Linear Regression

Linear regression in R is quite straightforward and there are excellent additional packages like visualizing the dataset. This concrete contribution provides an example based on free data represents a short tutorial of linear regresion using the R tool. In order to understand the material better, the analysis is structured according to the Cross Industry Standard Process for Data Mining (CRISP-DM). We apply the CRISP-DM because it is soundly based on the practical and real-world experience of how to conduct big data analysis and analytics. It also reveals a step-wise approach that is more like practical problem where questions are asked before the real data analysis really begins. For a more general introduction to this topic, please refer to our article linear regression analysis.

Business Understanding Phase

This phase focuses on understanding the objectives and requirements from a business perspective, then converting this knowledge into a linear regression problem including a preliminary plan designed to achieve the objectives. The specific objective of our example is to predict the median house value in suburbs around Boston. This predictive task takes advantage of various recorded facts that are given to us in a specific dataset introduced below. Facts about houses in the neighborhood include average number of rooms to general Information about the area such as percent of households with low socioeconomic status. This means that often objectives are derived from what data do you receive. Given the clear objective we thus need to understand the data at hand much better.

Data Understanding Phase

The free R MASS library contains the ‘Boston data set, which is our example dataset for using linear regression later. But before starting a regression analysis it is much more important to first gain insights about the data to understand it truly better. The data understanding phase typically starts with data collection and includes activities that enable the analyst to become familiar with the data, identify data quality problems, and discover first insights in the data. In order to obtain a data understanding, please use the following R commands:

> library(MASS)
> names(Boston)
Output:

[1] "crim"  "zn"  "indus"  "chas"  "nox"  "rm"  "age"  "dis"  "rad"  "tax"  "ptratio"  "black"  "lstat"  "medv"

This initial view on the data tells us that we have 13 values also named predictors available in our given dataset that we can use to predict the median house value (medv). But this also reminds us on the importance of metadata for a dataset in practice. For our concrete example we can rely on R to provide this metadata by using the following R command:

> ?Boston

This command typically opens a browser with the page title ‘Housing Values in Suburbs of Boston’ and shows metadata about the ‘Boston’ dataset. This metadata provides us with valuable pieces of information for our data understanding such as the unit (e.g. $ or sq.ft.) and what each attribute actually means:

crim (per capita crime rate by town)
zn (proportion of residential land zoned for lots over 25,000 sq.ft.)
indus (proportion of non-retail business acres per town)
chas (Charles River dummy variable (= 1 if tract bounds river; 0 otherwise))
nox (nitrogen oxides concentration (parts per 10 million))
rm (average number of rooms per dwelling)
age (proportion of owner-occupied units built prior to 1940)
dis (weighted mean of distances to five Boston employment centres)
rad (index of accessibility to radial Highways)
tax (full-value property-tax rate per \$10,000)
ptratio (pupil-teacher ratio by town)
black (1000(Bk – 0.63)^2, where Bk is the proportion of blacks by town)
lstat (lower status of the population (percent))
medv (median value of owner-occupied homes in \$1000s)

Data Preparation Phase

Given a profound understanding of the data and its structure we can start to prepare the data analysis. The data preparation phase covers all activities needed to construct the dataset that will be finally used from the initial raw data. These tasks are often performed multiple times and not in any prescribed order. Tasks include table, record, and attribute selection, as well as transformation and cleaning of data for modeling Tools like R. In our example we pick first an attributes that we believe is important to understand the relationship between facts and house values in the neighborhood: lstat – lower status of the population or in other words percent of households with low socioeconomic status. Experts also refer to this part of the process as ‘feature selection’ whereby the lstat attribute is considered to be a feature we base our prediction upon. As we can keep this attribute as it is we do not need to do anything in particular in R in this phase.

Modeling Phase

In the modeling phase typically various modeling techniques are selected and applied, and their parameters are calibrated to optimal values. Although there are usually several techniques for the same analysis problem we pick here the linear reqression technique out of many others. Some techniques have specific requirements on the form of data and thus it is usual to go back to the data preparation phase. Please use the following R command to perform the linear regression on our dataset:

> model.fit = lm(medv~lstat,data=Boston)

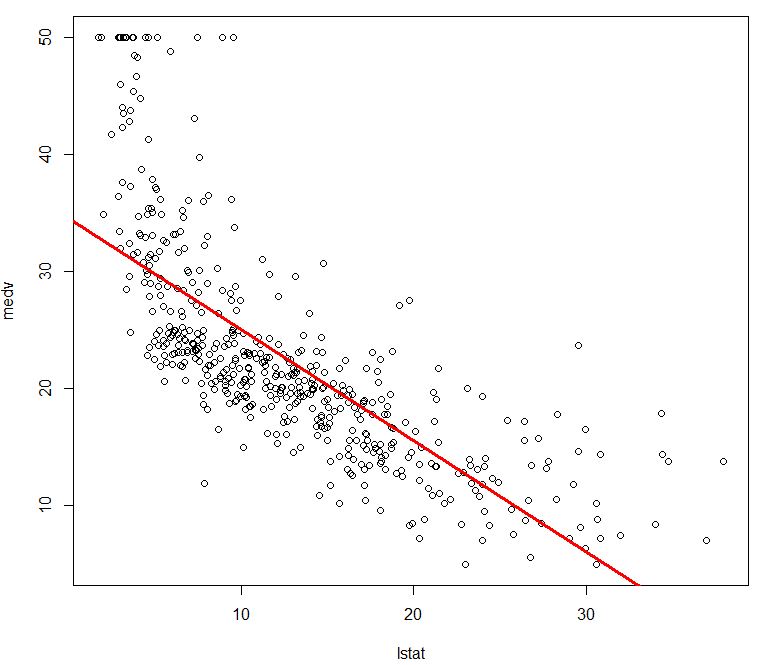
The command above is using the R lm() function to fit a linear regresion model. As we set in the previous phases above, we use the medv (median value of owner-occupied homes in \$1000s) as predictor and lstat as response. The general usage for linear regression in the tool R is therefore lm(y~x,data), where y is the response variable, x is the predictor variable, and data specifies our dataset ‘Boston’ in which the two attributes are stored. We visualize our interesting parts of the data with plot() R command and our fitted regression model using the abline() R command as follows:

> attach(Boston)
> plot(lstat,medv)
> abline (model.fit ,lwd =3, col =”red “)

Evaluation Phase

The evaluation phase start once there is a fitted a model that appears to have high quality from a data analysis perspective. But it is important to thoroughly evaluate the obtained linear regression model and review the steps executed to create it. This is important in order to be certain the regression model properly achieves the business objective: The specific objective of our example is to predict the median house value in suburbs around Boston.

Being a linear model the regression plot shows a red regression line. Given the line we are able to predict the median house value depending on the data of lstat – lower status of the population or in other words percent of households with low socioeconomic status. The Regression model line suggests that the higher the percent of households with low socioeconomic status, the lower the median house value. One can pick a certain percentage on the x-axis (socioeconomic status) and is able to roughly predict what is the value on the y-axis (house value).

There are more formal evaluations that can be performed such as the R^2 statistic and F-statistic for the model. Another alternative is to produce confidence intervals and prediction intervals for the model prediction and its evaluation. Please refer to our article ‘Confidence Interval’ for one example of assessing the quality of the model. More in-depth evaluations may hint to the fact that there is a non-linear relationship in the data and as such the linear regression model is not the perfect model for the data. The linear fit captures the essence of the data relationship but it is somewhat deficient in the top left of the plot and bottom right. Still linear regression is a very simple model and explains the basic relationship for the selected attributes medv and lstat nicely.

More Information about R Linear Regression

The following video provides another nice source of information:

Follow us on Facebook: