SVM – Support Vector Machine
A Support Vector Machine known as SVM is a classification technique developed around 1990 for data analysis. They perform very well in many settings and are considered as one of the best ‘out-of-the-box classifiers’.
Understanding the Margin
The key to understand this technique is a term called margin. The illustration below provides a simple way to understand this term. The figure uses a ‘simplified coordinate system‘ and uses a bit of linear algebra. The orange area represents the widest margin that seperates the positive from the negative samples. The orange samples, positive and negative samples, on the boundary are called support vectors because they support this margin. Many other samples in the figure are removed such as many red (-) and green (+) samples that are represented by just one sample each. In a practical situation there will be many more of them but as they are not directly on the boundary of the margin they are not support vectors. This is important since the non support vector samples can be ignored for a while because they do not help in creating and understanding the margin.
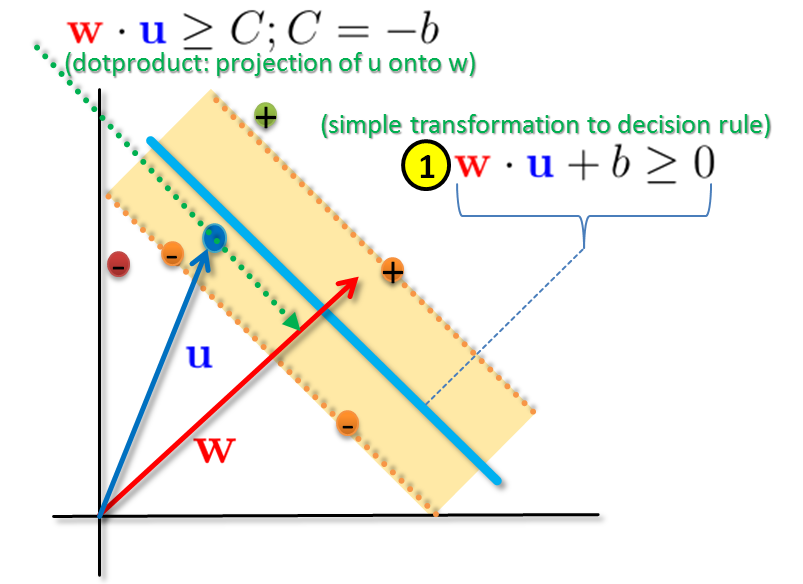
The vectors shown in the illustration above are helping us to create a more formal mathematical notation. The vector w is of ‘any length’ but needs to be perpendicular to the blue decision boundary. The vector u points to an unknown quantity representing a new unseen sample that we want to classify. In order to classify this new sample correctly we need to find out if the sample location is on the left or right side of the decision boundary. This means we need a decision rule that uses the blue decision boundary above. This is done by using the projection capabilities of dot products. In the illustration above we use vector u and take the green projection onto vector w. Depending on where this projection is it is left or right from the blue decision boundary. A simple transformation of this idea shown above as (1) provides the decision rule. The element (1) is the first important piece of understanding support vector machines.
More Information about SVM
A nice introduction to the topic is given in the following video:
Follow us on Facebook:











