Gradient Descent
Gradient descent refers to a technique in machine learning that finds a local minimum of a function. It is a quite general optimization technique used in many application areas. It can be used to minimize an error function in neural networks in order to optimize the weights of the neural network. While the technique can be used with more than one variable we illustrate here the basic idea using just one variable. In other words we look at 2D functions to minimize rather than 3D surfaces where gradient descent can be also succesfully applied.
Overall the human interpretation of this technique is often helpful to immagine first. This refers to a person that stands somewhere on a hill and wants to get as quickly as he can into the valley (aka local minima). He looks all around himself and, in ideal conditions, would go the steepest route downhill. This enables the person to arrive in the valley in the shortest time. Given this human interpretation of the problem assume that it is a blindfolded person that needs to figure out where the steepest descent really is. The person can assess its surrounding at a given position and takes one step at a time to eventually arrive in the valley. The gradient descent supports this process with the techniques described in the following paragraphs.
Understanding the term gradient
Consider the function below that has a certain slope in order to understand the word gradient first. At different given points x of this function there can be different gradients observed. At exactly point x1 we observe a ‘negative gradient’ and the function values in this direction are decreasing. At the point x2 we observe a very specific ‘zero gradient’ that refers to a stationary situation. The key goal of the gradient descent technique is to find such an x with ‘zero gradient’. Point x3 then refers to a ‘positive gradient’ and the function values in this direction are increasing. To sum up the gradient at any point x on the graph is given by the gradient of the red illustrated tangent to the graph at that point x. The gradient of a function is thus positive where the function is increasing and negative where the function is decreasing. Important for the gradient descent technique and for its convergence is that at the point x where the function reaches its minimum the red tangent is horizontal with a gradient that is zero.
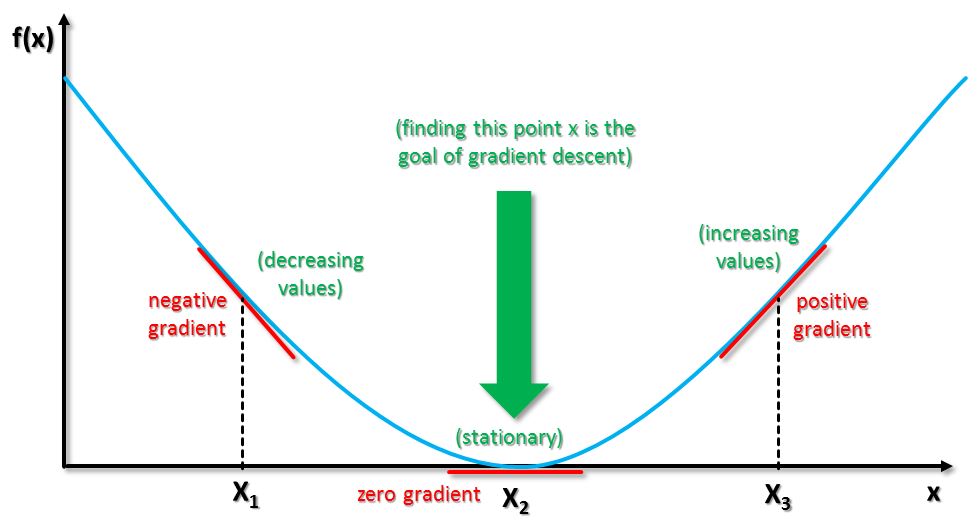
Understanding the term descent
The technique uses the mathematical fact that the derivative of a function f(x) evaluated at a point x is the gradient of that function at that point x. From the given figure above one can understand why the name of the technique is using the word ‘descent’ in order to find the minimum x of a given function. The technique is initialized with starting at some random point x. Then it takes the gradient of the function at that point x. With a specifically defined learning rate that is also called the step-size the technique performs one step in the negative direction of the gradient. This results in a newly picked point x most likely closer to the local minimum. The learning rate or step-size controls how big a step is and thus steers how fast we reach the local minimum. In other words if the learning rate parameter is big then we take big steps downhill and if the parameter is small then we take small steps downhill. Also this step-size can be reduced in order to not miss the local minima over time and eventually move beyond the local minima. The slope is most likely not as steep as before as we getting further towards the zero gradient and thus the reduced slope provides a reduced gradient. This in turn influences then the reduction of the step-size.
Afterwards the gradient of the function at that point is taken again and the aforementioned process is repeated until convergence. The technique will eventually converge where the gradient is zero. That means a so-called stationary point is found that corresponds to a local minimum. To sum up the technique moves iteratively with a step-size influenced by a weighting factor towards its goal of finding the local minima of a function. The function f(x) descreases fastest if one goes from current position a in the direction of the negative gradient of F at a. At the first step the position a is typically just guessed, set to zero, or a random initialization. Mathematically the whole technique can be defined by iteratively using the following formula:
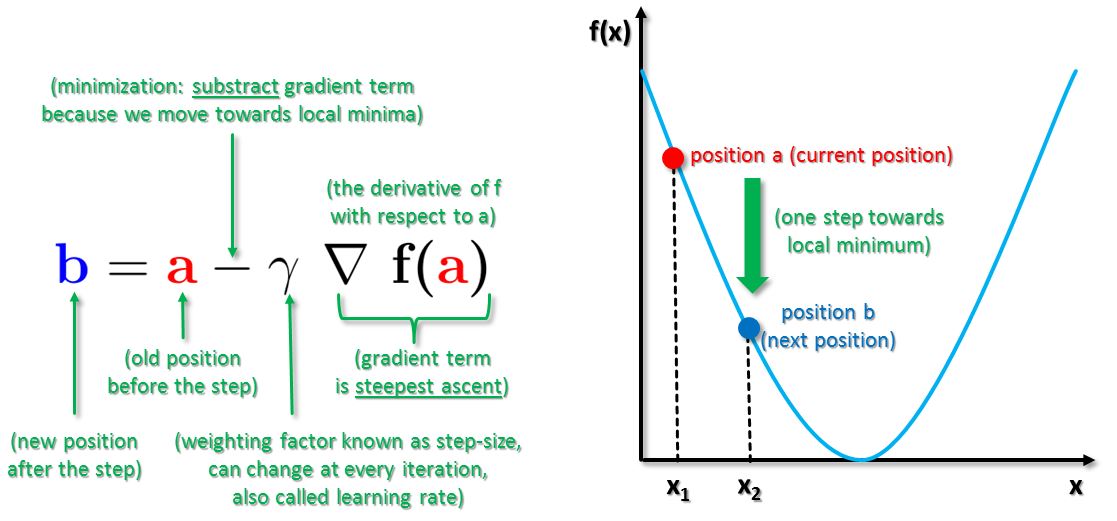
The above formula describes how gradient descent is used. In order to transfer this general formula to a concrete problem and to compute it to get a solution some calculus is needed and knowledge of partial derivations. In fact the derivative term in the formula above is sometimes also rewritten as seen below. The derivative term basically means a to create a red tangent at that point and it will provide a value for the slope of the red tangent to the function. Overall it is important to understand that we move in different directions for the next value for x based on this value. The slope in turn is computed by using the height divided by the horizontal value and it can be negative or positive depending on which particular point x is checked.

More information about gradient descent
The following video provides a good introduction to the gradient descent technique:
Follow us on Facebook:











